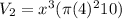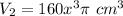Answer:
The volume of the new can is
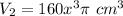
Explanation:
we know that
If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube
Let
z ----> the scale factor
In this problem

The volume of the original can is
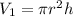
The volume of the new can is
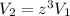
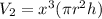
we have
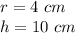
substitute