Answer:
The value of Cos 2a is - (
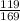 ) .
) .
Explanation:
Given as
Tan a =
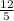
Now, ∵ Tan Ф =
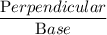
So, Tan a =
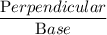
Or,
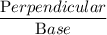 =
=
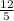
Or, From Pythagoras Theorem
Hypotenuse² = perpendicular² + Base²
Or, Hypotenuse² = 12² + 5²
Or, Hypotenuse² = 144 + 25
Or, Hypotenuse² = 169
∴ Hypotenuse =
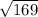 =
=
 13
13
Take Hypotenuse = 13
Now,∵ Cos 2Ф = Cos²Ф - Sin²Ф
So, Cos 2a = Cos²a - Sin²a
or , Cos 2a = 1 - 2 Sin²a ∵ Cos²a + Sin²a = 1
Or, Cos 2a = 1 - 2 ×(
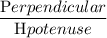 )²
)²
Or , Cos 2a = 1 - 2 ×(
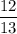 )²
)²
Or, Cos 2a = 1 - 2 × (
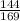 )
)
Or, Cos 2a = (
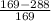 )
)
∴ Cos 2a = - (
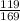 )
)
Hence the value of Cos 2a is - (
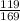 ) . answer
) . answer