Answer:
Because Alternate Interior angles are equal.
Explanation:
STEP - I:
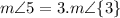
Reason:
This is the given data.
STEP - II:
It has multiplied and the reason is mentioned as well.
STEP - III:
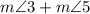 = 45° + 135° = 180°
= 45° + 135° = 180°
Reason:
It has substituted the value of
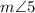 from the previous step. The sum of
from the previous step. The sum of
 and
and
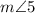 is 180°.
is 180°.
STEP - IV:

Reason:
We calculated
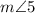 to be 135°.
to be 135°.
Note that
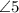 and
and
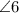 are on the same line. That means their sum should be 180°.
are on the same line. That means their sum should be 180°.
i.e.,
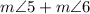 = 180°.
= 180°.
 135° +
135° +
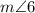 = 180°.
= 180°.
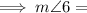 45°.
45°.
One of the ways to prove
 is to check if alternate interior angles are equal.
is to check if alternate interior angles are equal.
Here,
 and
and
 are alternate interior angles and they are equal.
are alternate interior angles and they are equal.
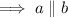 .
.