Question

A point p in the first quadrant lies on the parabola y=x^2. Express the coordinates of p as a function of the angle of inclination of the line joining p to the origin​

Answer 1

• The coordinates of the point p are:
  `(x,xtan\alpha )`

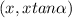
Step-by-step explanation:

1. Name the angle of inclination of the line joining p to the origin α.

2. Find the relation between the coordinates of the point (x,y)

When you draw a line from the origin to the parabola, the intersection point, p(x,y) will have coordinates (x,y).

As per the definition of the tangent trigonometric ratio you have:

• 
  `tan\alpha =(y)/(x)`

From which you can clear y:

• 
  `y=xtan\alpha =>(x,y)=(x,xtan\alpha )`

Which is the expression of the coordinates of p as a function of the angle of inclination of the line joining p to the origin.