Answer:
Distance between points
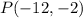 and
and
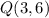 is 17 units
is 17 units
Explanation:
Given points:
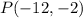
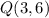
To determine the distance between points P and Q.
Steps to be carried out:
1) Plot the points P and Q on graph.
2) Construct a line from P towards right horizontally and a line from Q downwards vertically such that they meet at point
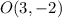
3) Join PQ thus forming a right triangle POQ.
4) We can find the distance of sides OP and OQ by counting the units between the points.
OP=

OQ=
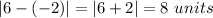
4)Now, we can apply Pythagorean theorem for triangle POQ.
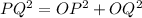 [
[
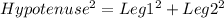 ]
]
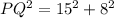

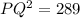
Taking square root both sides:
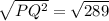
 [We take only the positive value as distance is always positive.
[We take only the positive value as distance is always positive.
∴ Distance between points
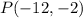 and
and
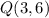 is 17 units
is 17 units