Question

Write an equation in slope - intercept form for the line that satisfies each set of conditions

passes through (-6, 15), parallel to the graph of 3x + 2y=1

passes through (5, -2), perpendicular to the graph of x + 2y = 8

Answer 1

see explanation

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

(1)

Rearrange 3x + 2y = 1 into this form by subtracting 3x from both sides

2y = - 3x + 1 ( divide all terms by 2 )

y = -
`(3)/(2)` x +
`(1)/(2)` ← in slope- intercept form

with slope m = -
`(3)/(2)`

Parallel lines have equal slopes, thus

y = -
`(3)/(2)` x + c ← is the partial equation

To find c substitute (- 6, 15) into the partial equation

15 = 9 + c ⇒ c = 15 - 9 = 6

y = -
`(3)/(2)` x + 6 ← equation of line

(2)

Rearrange x + 2y = 8 into slope- intercept form by subtracting x from both sides

2y = - x + 8 ( divide all terms by 2 )

y = -
`(1)/(2)` x + 4 ← in slope- intercept form

with slope m = -
`(1)/(2)`

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(-(1)/(2) )` = 2, thus

y = 2x + c ← is the partial equation

To find c substitute (5, - 2) into the partial equation

- 2 = 10 + c ⇒ c = - 2 - 10 = - 12

y = 2x - 12 ← equation of line

Answer 2

Answer: (1) y = -3x/2 + 6

(2) y = 2x - 12

Explanation:

The slope - intercept form is given as :

y = mx + c , where m is the slope and c is the y - intercept.

Two lines are said to be parallel if they have the same slope , that is if the slope of the first line is M1 and the slope of the second line is M2 , if they are parallel, M1 = M2.

(1) the equation of the given line is 3x + 2y = 1 , to find the slope of the line parallel to it , we must write the equation in slope - intercept form.

3x + 2y = 1

make y the subject of the formula

2y = -3x + 1

y = -3x/2 + 1/2

comparing with y = mx + c , the slope is -3/2 , we can now find the equation of the second line since the slope is known and it passes through the point (-6,15) using the formula:

y -
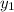`y_(1)` = m( x -
`x_(1)`)

y - 15 =
`(-3)/(2)` ( x -{-6} )

y - 15 =
`(-3)/(2)`(x + 6)

2 (y - 15) = -3 (x +6)

2y - 30 = -3x - 18

2y = -3x - 18 + 30

2y = -3x +12

y = -3x/2 + 6

This gives the equation that is parallel to 3x+2y = 1

(2) Two lines are said to be perpendicular if the product of their slope is -1 , that is if M1 is the slope of the first line and M2 is the slope of the second line , then M1.M2 = -1 , that is

`m_(1)` =
`(-1)/(m_(2) )`

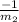
The equation of the line given is x + 2y = 8 , we have to write it in slope - intercept form to find the slope.

x + 2y = 8

2y = -x + 8

y = -x/2 + 4

The slope is -1/2 , the slope that is perpendicular to it is therefore 2.

We can now find the equation using the formula

y -
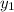`y_(1)` = m( x -
`x_(1)`)

y - (-2) = 2 ( x - 5)

y + 2 = 2x - 10

y = 2x -10 - 2

y = 2x - 12

Therefore , the equation of line perpendicular to x + 2y = 8 is y = 2x - 12