Answer:
232.6 metres after 3.8 seconds.
Explanation:
h(t) = -16t² + 122t
a = -16 b = 122 c = 0
Substitute into the quadratic formula
(Ignore the Â)
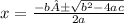

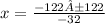
Split the equation at the ±
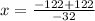
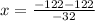
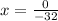


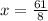
The two x-intercepts at 0 and 61/8. The midpoint of the x-intercepts is the axis of symmetry, which is the x-coordinate of the vertex.
Midpoint = [0 + (61/8)] / 2
Midpoint = 61/16 <= This is the time for maximum height
t = 61/16
t = 3.8125 => Round to t = 3.8
To find the maximum height, substitute t=61/16 into the equation
h(t) = -16t² + 122t
h(61/16) = -16(61/16)² + 122(61/16)
h(61/16) = 232.5625 => Round to h = 232.6
Therefore, the ball will reach the maximum height of 232.6 metres after 3.8 seconds.