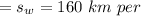Question

Flying against the wind, an airplane travels 2750 kilometers in 5 hours. Flying with the wind, the same plane travels 6090 kilometers in 7 hours. What is the rate

of the plane in still air and what is the rate of the wind?
Rate of the plane in still air:
Ola
1x
S
?
Rate of the wind:​

Answer 1

The rate of airplane in still air
`=710\ km\ hr^(-1)`

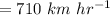
The rate of the wind is
`=160\ km \ hr^(-1)`

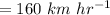
Explanation:

Let the speed of the airplane be
`s_(a)`

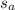
And the speed of the wind be
`s_(w)`

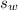
So we know that,
`Speed = (distance)/(time)`

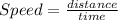
According to the question.

When the airplane is flying with the wind it will be supported by the wind.

So the speed,
`=s_(w)+s_(a) =(6090)/(7)`

`=s_(w)+s_(a) =870`

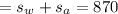
`=s_(w)=870-s_(a)`... equation (1)

When the airplane is flying with against the wind it will be negated by the wind.

Then the speed ,
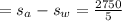`=s_(a)-s_(w)=(2750)/(5)`... equation (2)

Plugging the values from equation (1)....

`=s_(a)-(870-s_(a))=550`

`=2s_(a)=550+870`

`=2s_(a)=(550+870)/(2)=710`

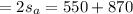
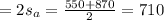
So rate of airplane in still air
`=710\ km\ per\ hr`

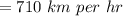
Now to find the rate of wind we can plug the values of rate of airplane in equation (1).

Then we have

`=s_(w)+s_(a) =870`

`=s_(w)=870-710=160`

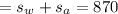
So the rate of the wind that is
`=s_(w)=160\ km\ per \hr`

The rate of airplane in still air
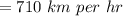`=710\ km\ per\ hr` and rate of the wind is
`=s_(w)=160\ km\ per\ \hr`