Answer:
The common ratio = 1/2
The sum of 9 terms of GP is 15,968.75
Explanation:
Here, in the given GP:
Firs Term a = 8000, Fifth term a(5) = 500
Let Common Ratio = r
Now, by the general term of GP:
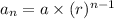
For, n = 5
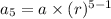
or,
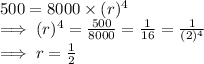
Hence in the given GP, a = 8000 and r = 1/2
Now, in a GP sum of n terms is
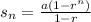
So, for n = 9,
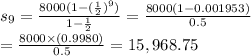
So,the sum of 9 terms of GP is 15,968.75.