Question

Bob makes his first $ 1, 100 deposit into an IRA earning 6.8 % compounded annually on his 24th birthday and his last $1, 100 deposit on his 36th birthday ​(13 equal deposits in​ all). With no additional​ deposits, the money in the IRA continues to earn 6.8 % interest compounded annually until Bob retires on his 65th birthday. How much is in the IRA when Bob​ retires?

Answer 1

$133991.2

Explanation:

Bob makes his first $1000 deposit into an IRA earning 6.8% compounded annually on his 24th birthday and his last $1000 deposit on his 36th birthday (13 equal deposits in all).

Therefore, till his retirement on his 65th birthday, the first deposit of $1000 will compound for (65 - 24) = 41 years.

His second deposit of $1000 will compound for 40 years and so on up to his 13th deposit of $1000, which will be compounded for ( 65 - 36) = 29 years.

Therefore, after retirement in his IRA there will be total

$
`[1000(1 + (6.8)/(100) )^(41) + 1000(1 + (6.8)/(100) )^(40) + 1000(1 + (6.8)/(100) )^(39) + ........ + 1000(1 + (6.8)/(100) )^(29)]` dollars

= $
`1000[1.068^(41) + 1.068^(40) + 1.068^(39) + .......... + 1.068^(29)]`

So, this is a G.P. whose number of terms is 13, the first term is
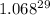`1.068^(29)` and common ratio is 1.068, then using formula for sum of G.P. we get,

= $
`1000* (1.068)^(29) [((1.068)^(13) - 1)/(1.068 - 1) ]`

= $
`(1000 * 6.74 * 19.88)`

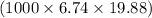
= $133991.2 (Answer)