Answer:
4.5 sq. units.
Explanation:
The given curve is
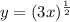
⇒
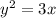 ...... (1)
...... (1)
This curve passes through (0,0) point.
Now, the straight line is y = 3x - 6 ....... (2)
Now, solving (1) and (2) we get,
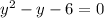
⇒ (y - 3)(y + 2) = 0
⇒ y = 3 or y = -2
We will consider y = 3.
Now, y = 3x - 6 has zero at x = 2.
Therefor, the required are =
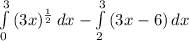
=
![√(3) [{\frac{x^{(3)/(2) } }{(3)/(2) } }]^(3) _(0) - [(3x^(2) )/(2) - 6x ]^(3) _(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7wr45jdis89awkrgtxke32uhjs5px2fvmb.png)
=
![[\frac{√(3)* 2 * 3^{(3)/(2) } }{3}] - [13.5 - 18 - 6 + 12]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fyf0cyfdpq1614xrz4tt3zovaq4nfxainv.png)
= 6 - 1.5
= 4.5 sq. units. (Answer)