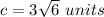Question

Find the diagonal of a square whose sides are of the given measure.
Given = 3v3

Answer 1

The measure of the diagonal is
`3√(6)\ units`

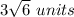
Explanation:

Let

c -----> the diagonal of a square in units

a ----> the length side of a square

Remember that a square can be divided into two congruent right triangles

see the attached figure to better understand the problem

Applying the Pythagoras Theorem

`c^(2)=a^(2)+a^(2)`

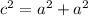
we have

`a=3√(3)\ units`

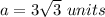
substitute

`c^(2)=(3√(3))^(2)+(3√(3))^(2)`

`c^(2)=54`

`c=√(54)\ units`

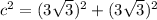
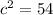
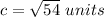
simplify

`c=3√(6)\ units`