Answer:
Distance between boat and light house = 134 m
Explanation:
Given data:
Height of light house = 46 m
Angle of elevation from boat to the top of light house = 19°
From the data given to us we can construct a right triangle ABC.
For the Δ ABC
AB= 46 m
∠C= 19°
We can apply trigonometric ratio to find side BC which is the distance of light house from the boat.
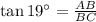
Multiplying both sides by BC.
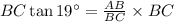
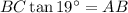
Dividing both sides by tan 19°
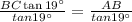

Substituting value of AB and tan 19°
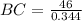

Distance between boat and light house = 134 m