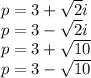Question

`( {p}^(2) - 6p {)}^(2) + 10( {p}^(2) - 6p) = 11`
​

Answer 1

There are four roots of
`p`,

`p= 3+√(2)i\\p = 3-√(2)i\\p= 3+√(10)\\p = 3-√(10)`

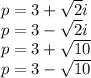
Step-by-step explanation:

Given:

`(p^2-6p)^2+10(p^2-6p)=11\\`

Let
`p^2-6p =x`

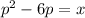
Now solving the equation we get:

`x^2+10x=11\\x^2+10x-11=0\\x^2-x+11x-11=0\\x(x-1)+11(x-1)=0\\(x+11)(x-1)=0`

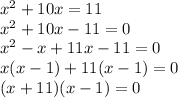
Now, solving for two values of
`x`, we get;

`x+11=0\\x=-11\\also; x-1=0\\x=1`

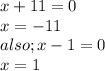
Now re-substituting value of
`x`, we get;

`p^2-6p=-11\\p^2-6p+11=0\\also p^2-6p=1\\p^2-6p-1=0\\`

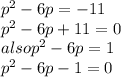
Now we have two quadratic equation we solve for each,

1) We will solve for
`p^2-6p+11=0`

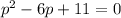
Using quadratic formula to solve it. This gives,

`x= \frac{-b\±√(b^2-4ac)} {2a}`

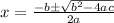
Here
`b= -6, a=1, c =11`

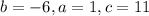
hence,
`p= \frac{-(-6)\±√((-6)^2-4* 1* 11)} {2* 1}=\frac{6\±√((36-44))} {2}=\frac{6\±√(-8)} {2}= \frac{6\±2√(2)i} {2}`

`p = \frac{6\±2√(2)i} {2}= 3\±√(2)i\\hence, p= 3+√(2)i \ or \ p = 3-√(2)i`

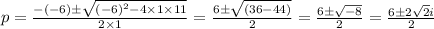
2) We will solve for
`p^2-6p-1=0`

Using quadratic formula to solve it. This gives,

`x= \frac{-b\±√(b^2-4ac)} {2a}`

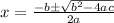
here
`b= -6, a=1, c =-1`

`\therefore p= \frac{-(-6)\±√((-6)^2-4* 1* -1)} {2* 1}=\frac{6\±√((36+4))} {2}=\frac{6\±√(40)} {2}= \frac{6\±2√(10)} {2}`

`p = \frac{6\±√(10)} {2}= 3\±√(10)\\hence, p= 3+√(10) \ or \ p = 3-√(10)`

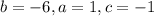
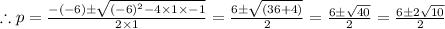
Hence, from 1 and 2, we find there are 2 real roots and 2 imaginary roots.

`p= 3+√(2)i\\p = 3-√(2)i\\p= 3+√(10)\\p = 3-√(10)`