Question

How would adding a score of zero affect the mean and mediam game scores

Answer 1

Here is the complete question attached with.

The mean score would decrease more than the median score.

Explanation:

The numbers for which we have to find the mean and median are:

`60,70,80,80,100`

Here the mean,
`(Sum\ of\ all\ observations)/(Number\ of all\ observations) =(60+70+80+80+100)/(5) =78`

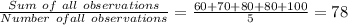
Median,
`=80` as median is the middle term if the observations are arranged in ascending order.

Now as the question says that we have to add a zero to see its effect.

So adding a zero we have

Mean
`=(0+60+70+80+80+100)/(6) =65`

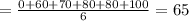
Median
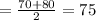`= (70+80)/(2) =75`,as number of observations is even terms so we will add two middle numbers and divide it with
`2`.

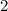So we can conclude that the mean is having more variation than the median.

Mean shows as variation of
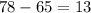`78-65=13` where as Median shows a variation of
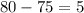`80-75=5` only.

So our final answer is option D that is "The mean score would decrease more than the median score."