Question

Is x^3+3x an even or odd function and is it symmetric in respect to the y-axis, origin, or neither

Answer 1

Answer:
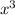`x^(3)` + 3x is an odd function and it is symmetric about the origin.

Explanation:

A function is odd if the graph of the function is symmetrical about the origin, or a function is odd if f(-x) = -f(x). To determine if a function is even or odd, you substitute -x for x in the function, if the resulting function is the same as the original function, then the function is even but if otherwise , the function is odd. Considering the graph of
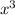`x^(3)` + 3x , it is symmetric about the origin , therefore it is an odd function.

Considering the second method of checking , let us substitute -x for x in the equation.

`x^(3)` + 3x

`(-x)^(3)` + 3(-x)

=
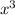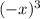`-x^(3)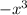` - 3x , this shows clearly that it is an odd function.