Question

A student in Greece discovers a pottery bowl

that contains 21% of its original amount of C-
14.
N = Noe-kt
No = inital amount of C-14 (at time t = 0)
N = amount of C-14 at timet
t = time, in years
k = 0.0001

age of the pottery bowl to the nearest year??

Answer 1

The age of the pottery bowl to the nearest year is 15606 years.

Explanation:

Let the initial amount of C-14 in the bowl i.e.
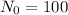`N_(0) = 100` and today (say after t years) the amount of C-14 in the bowl i.e. N = 21.

Therefore, from the given equation we can write

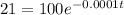`21 = 100 e^(- 0.0001t)` {Since, k is give to be 0.0001}

⇒
`0.21 = e^(- 0.0001t)`

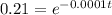
Now, taking ln on both sides we get

ln 0.21 = - 0.0001t (ln e) {Since,
`\ln a^(b) = b \ln a`}

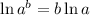⇒ - 1.560647 = - 0.0001t {We have ln e = 1}

⇒ t = 15606.47 years ≈ 15606 years

Therefore, the age of the pottery bowl to the nearest year is 15606 years.(Answer)