Question

The quadratic function

R(p)= -5.2p^2 + 65p - 75

gives the amount of revenue R(p) in dollars generated by a product priced at p dollars.

Question: What is the maximum revenue that can be generated?

Answer 1

The maximum revenue that can be generated is $128.13

Explanation:

we have

`R(p)=-5.2p^(2)+65p-75`

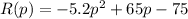
where

R(p) represent the amount of revenue in dollars

p the product price

This is a vertical parabola open downward

The vertex represent a maximum

so

The y-coordinate of the vertex represent the maximum revenue that can be generated

Solve by graphing

using a graphing tool

Graph the quadratic equation

The vertex is the point (6.25,128.125)

see the attached figure

the y-coordinate of the vertex is 128.125

therefore

The maximum revenue that can be generated is $128.13