Answer:
(1, 4)
Explanation:
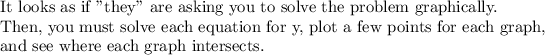

Below are a few points for Equations (1) and (2).}
Equation (1) is the blue line in the graph below.
Equation (2) is the red line.
The two lines cross at the black dot
Your four points are labelled . The one that is closest to the intersection is (1, 4).
The approximate solution to the system of equations is (1, 4).