Question

Identify the asymptotes of each function. 1/(x-3) - 6

Answer 1

`\bf \cfrac{1}{x-3}-6\implies \stackrel{\textit{using the LCD of x-3}}{\cfrac{1-(x-3)6}{x-3}}\implies \cfrac{1-6x+18}{x-3}\implies \cfrac{-6x+19}{x-3}`

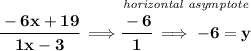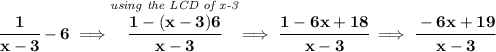
for the vertical asymptote, we simply zero out the denominator and solve for "x"

x - 3 = 0

x = 3 <---- that's the only vertical asymptote

for the horizontal asymptote, well, let's notice the degrees of the numerator and denominator, in this case, the degree of the numerator is 1, and the degree of the denominator is 1, thus when that occurs, the horizontal asymptote occurs at the fraction from the leading terms' coefficients.

`\bf \cfrac{-6x+19}{1x-3}\implies \stackrel{\textit{horizontal asymptote}}{\cfrac{-6}{1}\implies -6 = y}`