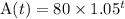Question

A manufacturing plant earned $80 per man-hour of labor when it opened. Each year, the plant earns an additional 5% per man-hour.Write a function that gives the amount A(t) that the plant earns per man-hour t years after it opens.

Answer 1

A function that gives the amount that the plant earns per man-hour t years after it opens is
`\mathrm{A}(\mathrm{t})=80 * 1.05^{\mathrm{t}}`

Solution:

Given that

A manufacturing plant earned $80 per man-hour of labor when it opened.

Each year, the plant earns an additional 5% per man-hour.

Need to write a function that gives the amount A(t) that the plant earns per man-hour t years after it opens.

Amount earned by plant when it is opened = $80 per man-hour

As it is given that each year, the plants earns an additional of 5% per man hour

So Amount earned by plant after one year = $80 + 5% of $80 = 80 ( 1 + 0.05) = (80 x 1.05)

Amount earned by plant after two years is given as:

`=(80 * 1.05)+5 \% \text { of }(80 * 1.05)=(80 * 1.05)(1.05)=80 * 1.052`

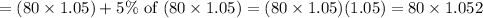
Similarly Amount earned by plant after three years
`=80 * 1.05^(t)`

`\begin{array}{l}{\Rightarrow \text { Amount earned by plant after } t \text { years }=80 * 1.05^(t)} \\\\ {\Rightarrow \text { Required function } \mathrm{A}(t)=80 * 1.05^(t)}\end{array}`

Hence a function that gives the amount that the plant earns per man-hour t years after it opens is
`\mathrm{A}(t)=80 * 1.05^(t)`