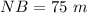Question

How to solve the problems​

Answer 1

1. 79°

2. 54°

3. 107.5°

4. 44°, 35 cm

5. 76°, 3.5 cm

6. m∠U=36°, m∠M=m∠D=72°, MD=8.6 cm

7. 78°, 93 cm

8. 81°, 75 cm

Explanation:

1. The diagram shows an isosceles triangle because TH = OT. Angles adjacent to the base OH of isosceles triangle are congruent, so

`m\angle H=m\angle O`

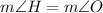
The sum of the measures of all interior angles is always 180°, thus

`m\angle H+m\angle O+m\angle T=180^(\circ)\\ \\2m\angle H+22^(\circ)=180^(\circ)\\ \\2m\angle H=180^(\circ)-22^(\circ)\\ \\2m\angle H=158^(\circ)\\ \\m\angle H=79^(\circ)`

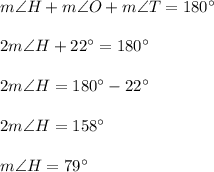
2. The diagram shows an isosceles triangle DGO because DG = GO. Angles adjacent to the base DO of isosceles triangle are congruent, so

`m\angle D=m\angle O=63^(\circ)`

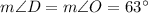
The sum of the measures of all interior angles is always 180°, thus

`m\angle D+m\angle O+m\angle G=180^(\circ)\\ \\63^(\circ)+63^(\circ)+m\angle G=180^(\circ)\\ \\m\angle G=180^(\circ)-63^(\circ)-63^(\circ)\\ \\m\angle G=54^(\circ)`

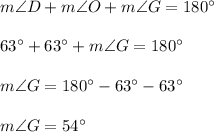
3. The diagram shows an isosceles triangle SLO because LO = SO. Angles adjacent to the base SL of isosceles triangle are congruent, so

`m\angle S=m\angle L`

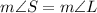
The sum of the measures of all interior angles is always 180°, thus

`m\angle S+m\angle L+m\angle O=180^(\circ)\\ \\2m\angle L+35^(\circ)=180^(\circ)\\ \\2m\angle L=180^(\circ)-35^(\circ)\\ \\2m\angle L=145^(\circ)\\ \\m\angle L=72.5^(\circ)`

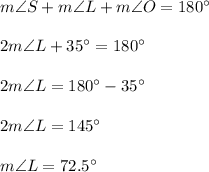
Angles OLE and L (SLO) are supplementary (add up to 180°), so

`m\angle OLE=180^(\circ)-m\angle L\\ \\m\angle OLE=180^(\circ)-72.5^(\circ)\\ \\m\angle OLE=107.5^(\circ)`

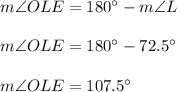
4. The diagram shows an isosceles triangle AMR because
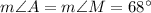`m\angle A=m\angle M=68^(\circ)` (angles adjacent to the side AM are congruent, so triangle AMR is isoseceles).

The sum of the measures of all interior angles is always 180°, thus

`m\angle A+m\angle M+m\angle R=180^(\circ)\\ \\m\angle R+2\cdot 68^(\circ)=180^(\circ)\\ \\m\angle R=180^(\circ)-2\cdot 68^(\circ)\\ \\m\angle R=44^(\circ)`

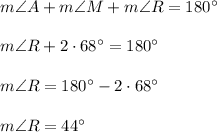
To legs in isosceles triangle are always congruent, so

`RM=AR=35\ cm`

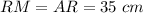
5. The diagram shows isosceles triangle RYD because YD = RD. Angles adjacent to the base RY are congruent, so

`m\angle R=m\angle Y`

The sum of the measures of all interior angles is always 180°, thus

`m\angle R+m\angle Y+m\angle D=180^(\circ)\\ \\2m\angle Y+28^(\circ)=180^(\circ)\\ \\2m\angle Y=180^(\circ)-28^(\circ)\\ \\2m\angle Y=152^(\circ)\\ \\m\angle Y=76^(\circ)`

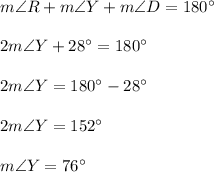
To legs in isosceles triangle are always congruent, so

`YD=RD=3.5\ cm`

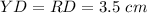
6. The diagram shows an isosceles triangle UMD because UM = UD. Angles adjacent to the base MD of isosceles triangle are congruent, so

`m\angle D=m\angle M=72^(\circ)`

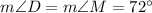
The sum of the measures of all interior angles is always 180°, thus

`m\angle D+m\angle M+m\angle U=180^(\circ)\\ \\72^(\circ)+72^(\circ)+m\angle U=180^(\circ)\\ \\m\angle U=180^(\circ)-72^(\circ)-72^(\circ)\\ \\m\angle U=36^(\circ)`

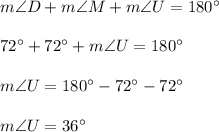
To legs in isosceles triangle are always congruent, so

`UM=UD=14\ cm`

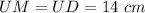
The perimeter of isosceles triangle MUD is 36.6 cm, so

`UM+MD+UD=36.6\\ \\MD=36.6-14-14\\ \\MD=8.6\ cm`

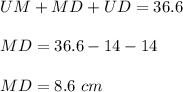
7. The sum of the measures of all interior angles is always 180°, thus

`m\angle T+m\angle S+m\angle B=180^(\circ)\\ \\m\angle T+78^(\circ)+24^(\circ)=180^(\circ)\\ \\m\angle T=180^(\circ)-78^(\circ)-24^(\circ)\\ \\m\angle T=78^(\circ)`

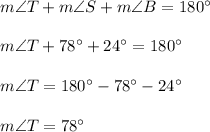
Triangle STB is isosceles triangle because
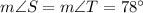`m\angle S=m\angle T=78^(\circ)` (angles adjacent to the side ST are congruent, so triangle STB is isoseceles).

To legs in isosceles triangle are always congruent, so

`SB=TB\\ \\y+22.5=38.5\\ \\y=38.5-22.5\\ \\y=16`

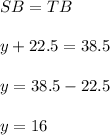
Hence,

`ST=16\ cm\\ \\TB=SB=38.5\ cm`

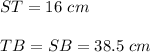
and the perimeter of triangle STB is

`P_(STB)=16+38.5+38.5=93\ cm`

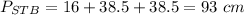
8. The diagram shows isosceles triangle CNB because CN = CB. Angles adjacent to the base RY are congruent, so

`m\angle N=m\angle B`

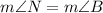
The sum of the measures of all interior angles is always 180°, thus

`m\angle N+m\angle B+m\angle C=180^(\circ)\\ \\2m\angle N+18^(\circ)=180^(\circ)\\ \\2m\angle N=180^(\circ)-18^(\circ)\\ \\2m\angle N=162^(\circ)\\ \\m\angle N=81^(\circ)`

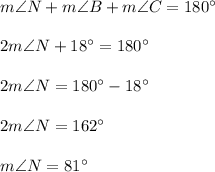
To legs in isosceles triangle are always congruent, so

`CB=CN=2x+90\ m`

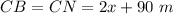
The perimeter of the triangle CNB is

`2x+90+2x+90+x=555\\ \\5x+180=555\\ \\x+36=111\\ \\x=111-36\\ \\x=75\ m`

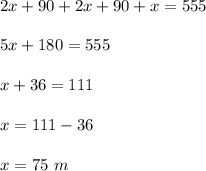
So,
`NB=75 \ m`