Answer:
43 faculty tickets and 87 student tickets
Explanation:
Let x be the number of faculty tickets sold and y be the number of student tickets sold.
130 tickets were purchased, so
x + y = 130
The cost of faculty ticket was $16.50, then x tickets cost $16.50x.
The cost of student tickets sold was $9.90, then y tickets cost $9.90y.
A total of $ 1,570.80 was collected, thus
16.50x + 9.90y = 1,570.80
You get the system of two equations:
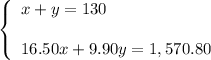
From the first equation:
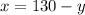
Substitute it into the second equation:
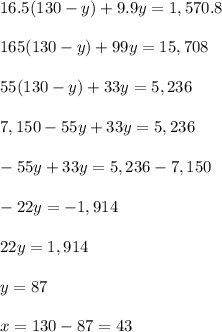
43 faculty tickets and 87 student tickets