Question

2. y = -2x² + 8x
Axis of Symmetry:
Vertex:
Domain:
Range:​

Answer 1

Part 1) The axis of symmetry is x=2

Part 2) The vertex is the point (2,8)

Part 3) The domain is all real numbers

Part 4) The range is all real numbers less than or equal to 8

Explanation:

we have

`y=-2x^(2)+8x`

This is a vertical parabola open downward (because the leading coefficient is negative)

The vertex represent a maximum

step 1

Find the vertex

Convert the quadratic equation in vertex form

Factor -2 leading coefficient

`y=-2(x^(2)-4x)`

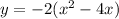
Complete the square

`y=-2(x^(2)-4x+4)+8`

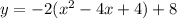
rewrite as perfect squares

`y=-2(x-2)^(2)+8`

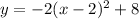
so

The vertex is the point (2,8)

step 2

Find the axis of Symmetry

we know that

In a vertical parabola, the axis of symmetry is equal to the x-coordinate of the vertex

the vertex is the point (2,8)

therefore

The axis of symmetry is x=2

step 3

Find the domain

The domain of the quadratic equation is the interval ------> (-∞,∞)

The domain is all real numbers

step 4

Find the range

The range of the quadratic equation is the interval ------> (-∞,8]

`y\leq 8`

The range is all real numbers less than or equal to 8