Answer:
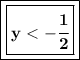
Option A
Explanation:
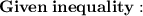
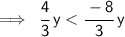
We need to find the solution to the inequality.
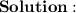
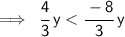
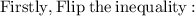
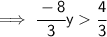
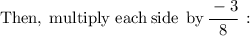
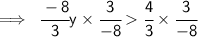
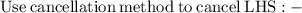
Steps of cancelling :-
- Cancel -8( which is on the numerator) and -8 (on the denominator) :
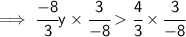
- Cancel 3(which is on the numerator) and 3( which is on the denominator) :
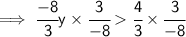
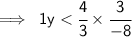
As we know 1y equals to y. So,
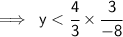
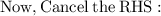
Steps of cancelling:-
- Cancel 3 (which is on the numerator) and cancel 3 (which is on the denominator):
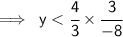
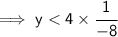
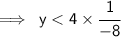
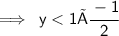
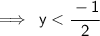
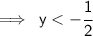
This matches with option A.
Hence, Option A is correct!

I hope this helps!
Let me know if you have any questions.I am joyous to help!