Question

How much energy in (kJ) is required to decompose 14.7 g of CaCO3.

CaCO3(s) + 556 kJ > CaO(s) + CO2(g)

Answer 1

81.732 kilo Joules of energy is required to decompose 14.7 grams of calcium carbonate.

Step-by-step explanation:

Moles of calcium carbonate =
`(14.7 g)/(100 g/mol)=0.147 mol`

`CaCO_3(s) + 556 kJ\rightarrow CaO(s) + CO_2(g)`

According to reaction, 1 mole of calcium carbonate requires 556 kilo Joules of energy to decompose:

Then 0.147 moles of calcium carbonate will need:

`0.147 * 556 kJ=81.732 kJ`

81.732 kilo Joules of energy is required to decompose 14.7 grams of calcium carbonate.

Answer 2

81.732KJ

Step-by-step explanation:

Reaction : CaCO₃(s) → CaO(s) + CO₂(g), +556KJ

⇒To decompose 1 mole of CaCO₃, 556KJ of energy is required

The molecular weight of CaCO₃ is 40 + 12 + 3×16

⇒ molecular weight of CaCO₃ = 100 g

∴ 100 g of CaCO₃ requires 556KJ of energy

Need to find out how much energy is required by 14.7 g of CaCO₃

⇒
`(100)/(14.7)` =
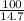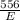
`(556)/(E)`

⇒ E =
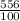`(556)/(100)`×14.7 KJ = 81.732 KJ

∴ Energy required to decompose 14.7 g of CaCO₃ is 81.732 KJ