Question

a boutique handmade umbrella factory currently sells 22500 umbrellas per year at a cost of 9 dollars each. in the previous year when they raised the price to 16 dollars, they only sold 12000 umbrellas that year. assuming the amount of umbrellas sold is in a linear relationship with the cost, what is the maximum revenue?

Answer 1

The revenue will be maximum when the price of each umbrella will be $12.

Explanation:

Let the number of umbrellas sold n(c) is a linear function of the cost of each umbrella (c, say).

And the relation is n(c) = xc + y ......... (1)

Now, at c = 9 dollars, n(9) = 22500 and at c = 16 dollars, n(16) = 12000

Hence, from the equation (1) we get

22500 = 9x + y ........ (2) and

12000 = 16x + y .......... (3)

Hence, from equations (2) and (3) we get (16x - 9x) = -10500

⇒ 7x = -10500

⇒ x = -1500

Now, from equation (2), we get 22500 = 9 × (-1500) + y

⇒ y = 36000

Therefore, the relation is n(c) = - 1500c + 36000

Now, the revenue will be given by R = n(c) × c = - 1500c² + 36000c

Condition for maximum revenue is
`(dR)/(dc) = 0 = -3000c + 36000`

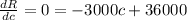
⇒ c = 12 dollars.

Therefore, the revenue will be maximum when the price of each umbrella will be $12. (Answer)