Question

Given: ΔАВС, m∠ACB = 90°

CD
⊥
AB
, m∠ACD = 60°,BC = 6 cm
Find CD, Area of ΔABC

Answer 1

CD=3√3

Explanation:

Answer 2

CD = 5.196 cm

Area = 31.177 sq. cm.

Explanation:

See the attached diagram.

Given that ∠ ACB = 90° in Δ ABC.

Now, CD ⊥ AB and ∠ CDB = ∠ CDA = 90°

Given that ∠ ACD = 60° and BC = 6 cm.

We have to find the length of CD and the area of Δ ABC.

Now, ∠ CAD = 90° - ∠ ACD = 90° - 60° = 30°

Again, ∠ CBD = 90° - ∠ CAD = 90° - 30° = 60°.

Now, from Δ BCD,
`\sin 60 = (CD)/(BC) = (CD)/(6)`

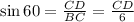
{Since Δ BCD is a right triangle and ∠ CDB = 90°}

⇒
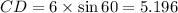`CD = 6 * \sin 60 = 5.196` cm. (Answer)

Now, from Δ ACD,
`\sin 30 = (CD)/(AC) = (5.169)/(AC)`

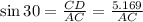
{Since Δ ACD is a right triangle and ∠ ADC = 90°}

⇒
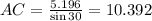`AC = (5.196)/(\sin 30) = 10.392` cm

So, the area of Δ ABC =
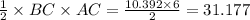`(1)/(2) * BC * AC = (10.392 * 6)/(2) = 31.177` sq. cm. (Answer)