The prepayment fee of $6182.58 would be charged to Artemis for paying off her loan 16 years early.
Answer: Option C
Explanation:
30 year loan at 9.6% interest yields.
Number of month = 30 (12) = 360 months
Annual percent interest of
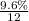 = monthly percent interest of .8%
= monthly percent interest of .8%
The formula for the present value of an ordinary annuity, as opposed to an annuity due, is as follows

With r and n adjusted for periodicity, where
P = the present value of an annuity stream
PMT = the dollar amount of each annuity payment
r = the interest rate (also known as the discount rate)
n = the number of periods in which payments will be made
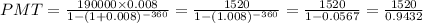
PMT = $1611.50 per month
Her loan 16 year early. It means
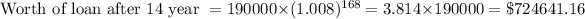
Worth of monthly payments for 14 year
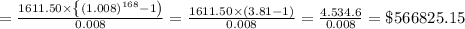
Amount still owed after 14 year = difference of the above two
=$724641.16 - $566825.18
=$157816.01
Prepayment fee =
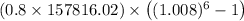
= 126252.82 (1.049-1) = 126252.82 (1.0489-1) = $6182.63