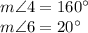Answer:
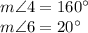
Explanation:
From the graph, we can say that
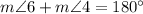
Because they are consecutive interior angles, and they sum 180° by definition. So, the reason of third statement is "by definition of consecutive interior angles".
We already know that
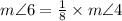
But,
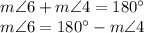
Replacing this, we have
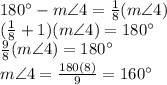
Then,
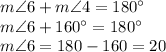
Therefore, the measures of these two angles are