Answer:
 or
or
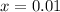
Explanation:
We are given a logarithmic equation of x and we have to solve it for x.
Given,
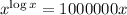
⇒
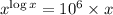
Now, taking log on both sides, we get
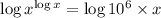
⇒
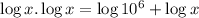
{Since
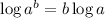 and
and
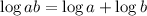 }
}
⇒
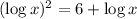
{Since log 10 = 1}
⇒ a² = 6 + a {Where, a = log x}
⇒ a² - a - 6 = 0
⇒ (a - 3)(a + 2) = 0
⇒ a = 3 or a = -2
⇒
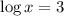 or
or
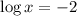
Now, converting logarithm to exponential form, we get,
⇒
 or
or
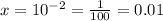 (Answer)
(Answer)