Question

A dinner was held to raise money for a children’s

museum. A ticket for one person cost $200 and a
ticket for a couple (two people) cost $350. A total of
130 people attended the dinner, and the ticket sales
total was $24,000. What is the total number of tickets
that were sold?

Answer 1

Total Number of tickets sold is 90.

Explanation:

Given:

Cost for 1 person ticket =
`\$200`

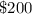
Cost for Couples ticket =
`\$350`

Let the number of 1 person attended dinner be
`x`.

Also Let the number of Couples attended dinner be
`y`

Total number of people attended dinner = 130

`x+2y=130 \ \ \ \ equation \ 1`

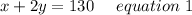
Now Ticket sale =
`\$24000`

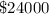
Hence,

`200x + 350y =24000\\`

Dividing both sides by 50 we get,

`(50(4x+7y))/(50)=\frac {24000}{50}\\4x+7y=480 \ \ \ \ \ equation \ 2`

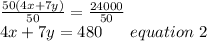
Multiplying equation 1 by 4 we get,

`x+2y=130 \\4(x+2y)=130 * 4 \\4x+8y= 520 \ \ \ \ \ equation \ 3`

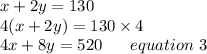
Subtracting equation 2 by equation 3 we get;

`(4x+8y= 520)-(4x+7y=480)\\y = 40`

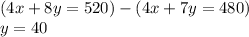
Now Substituting value of y in equation 1 we get;

`x+2y=130\\x+2* 40 =130\\x+80 =130\\x =130-80\\x=50\\`

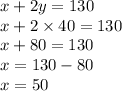
Hence total number of tickets sold =
`x+y =40 +50 =90`

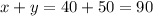
Total Number of tickets sold is 90.