Question

In a two-digit number the units digit is three less than the tens digit. If the digits are reversed, the sum of the reversed number and the original number is 121. Find the original number.

Answer 1

answer: 74

explanation:

7-3=4

74

+47

---

121

Answer 2

The digits are 7 and 4. The number would be 74.

Explanation:

In a two-digit number we have the unit's digit and the ten's digit. The unit's digit is represented by
`u`. Then ten's digit must be represents with a number 10 as a coefficient, and the variable would be
`d`. So, the numerical vale of the number would be:

`10d+u`

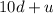
Also, we know that
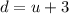`d=u+3`, because the unit digit is three less than tens digit, or tens digit is three more units than the unit digit.

Then, the sum of the reversed number and the original number is 121, this would be expressed:

`10d+u+10u+d=121\\11d+11u=121`

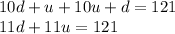
But, we know that
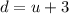`d=u+3`, so, we replace it:

`11(u+3)+11u=121\\11u+33+11u=121\\22u+33=121\\22u=121-33\\u=4`

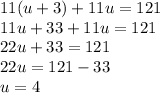
Then, if tens digits is 3 more,
`d=7`

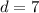
Therefore, the digits are 7 and 4. The number would be 74.