Question

Determine the values of k and p so that the solution is "All Reals" when solving for y:


`81y - 17 = k {}^2y + 6 + p`
​

Answer 1

The value of k is
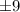`\pm 9` and The value of p is - 23

Explanation:

Given equation as :

81 y - 17 = k² y + 6 + p

The equation has real solution ,

Now for real solution the equation have no solution

∵ The equation has no solution the ,

The coefficient of y must be equal

I.e 81 = k²

Or, k =
`√(81)`

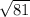
∴ k =
`\pm 9`

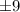
Again , If the coefficient of y is same then the equation is written as

6 + p = - 17

or, p = - 17 - 6

or, p = - 23

Hence The value of k is
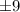`\pm 9` and The value of p is - 23 Answer