Answer:
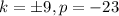
Explanation:
Given:
The equation is:
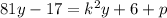
Here, the left hand side of the equation will be equal to that of the right hand side only if the coefficients of 'y' are same on both sides and the constant terms are also equal to each other.
Therefore,
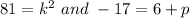
Solving each for 'k' and 'p'.
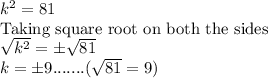

Therefore, the values of 'k' are -9 and 9. Value of 'p' is -23.