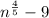For this case we have that by definition, a rational exponent is an exponent that can be expressed as
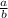 , where a and b are integers and n is nonzero.
, where a and b are integers and n is nonzero.
The exponent
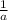 indicates the "a" root.
indicates the "a" root.
![x ^ {\frac {1} {a}} = \sqrt [a] {x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/a0f3e5soynqmnkidg3w0fdcp7nn05by5x0.png)
We have the following expression:
![\sqrt [5] {n ^ 4} + 3-12 =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/q45q5hiathxxuiqu94o4fw613ab7se6w8a.png)
Different signs are subtracted and the sign of the major is placed:
![\sqrt [5] {n ^ 4} -9 =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fireredkfciv2v9rf6whvjrmrn15grehsr.png)
Applying the property:
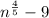
Answer: