Question

(a) Calculate the magnitude of the gravitational force exerted on a 1,320-kg satellite that is a distance of two earth radii from the center of the earth. N

(b) What is the magnitude of the gravitational force exerted on the earth by the satellite? N
(c) Determine the magnitude of the satellite's acceleration. m/s2
(d) What is the magnitude of the earth's acceleration? m/s2 Additional Materials

Answer 1

(a) 3224.27 N

(b) 3224.27 N

(c) 2.443 m/s^2

(d) 5.37 x 10^-22 m/s^2

Step-by-step explanation:

Mass of satellite, m = 1320 kg

mas of earth, M = 6 x 10^24 kg

Radius of earth, r = 6.4 x 10^6 m

(a) The force of gravitation between the earth and the satellite is given by

`F=G(Mm)/(d^(2))`

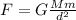
where, d is the distance between the two objects

`F=6.67*10^(-11)(6*10^(24)* 1320)/(\left (2* 6.4* 10^(6)  \right )^(2))`

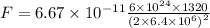
F = 3224.27 N

(b) The force on earth is same as the force on satellite.

F = 3224.27 N

(c) Acceleration of satellite = Force on satellite / mass of satellite

Acceleration of satellite = 3224.27 / 1320 = 2.443 m/s^2

(d) Acceleration of earth = Force on earth / mass of earth

Acceleration of satellite = 3224.27 / (6 x 10^24) = 5.37 x 10^-22 m/s^2