Question

Which of these sets could represent the side lengths of a right triangle?

Group of answer choices

{4, 8, 12}

{6, 8, 10}

{6, 8, 15}

{5, 7, 13}

Answer 1

{6, 8, 10} is a set which represents the side length of a right triangle.

Explanation:

In a right triangle:

`(Base)^(2)  + (Perpendicular)^(2)   = (Hypotenuse)^(2)`

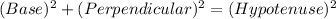
Now, in the given triplets:

(a) {4, 8, 12}

Here,
`(4)^(2)  + (8)^(2)   = 16 + 64  = 80\\\implies H = √(80)  =  8.94`

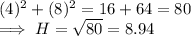
So, third side of the triangle 8.94 ≠ 12

Hence, {4, 8, 12} is NOT a triplet.

(b) {6, 8, 10}

Here,
`(6)^(2)  + (8)^(2)   = 36 + 64  = 100\\\implies H = √(100)  =  10`

So, third side of the triangle 10

Hence, {6, 8, 10} is a triplet.

(c) {6, 8, 15}

Here,
`(6)^(2)  + (8)^(2)   = 36 + 64  = 100\\\implies H = √(100)  =  10`

So, third side of the triangle 10 ≠ 15

Hence, {6, 8, 15} is NOT a triplet.

(d) {5, 7, 13}

Here,
`(5)^(2)  + (7)^(2)   = 25 + 49  = 74\\\implies H = √(74)  =  8.60`

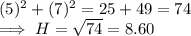
So, third side of the triangle 8.60 ≠ 13

Hence, {5, 7, 13} is NOT a triplet.