Answer with Explanation:
Mass of block=1.1 kg
Th force applied on block is given by
F(x)=
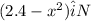
Initial position of the block=x=0
Initial velocity of block=
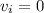
a.We have to find the kinetic energy of the block when it passes through x=2.0 m.
Initial kinetic energy=
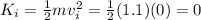
Work energy theorem:
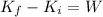
Where
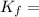 Final kinetic energy
Final kinetic energy
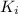 =Initial kinetic energy
=Initial kinetic energy
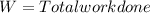
Substitute the values then we get
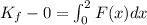
Because work done=
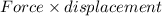
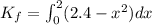
![K_f=[2.4x-(x^3)/(3)]^(2)_(0)](https://img.qammunity.org/2020/formulas/physics/college/qbi1nomvz8ej2p03j6wa1cvyiw6prgeg1a.png)
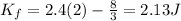
Hence, the kinetic energy of the block as it passes thorough x=2 m=2.13 J
b.Kinetic energy =
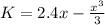
When the kinetic energy is maximum then
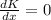
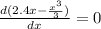
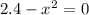
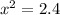
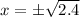
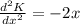
Substitute x=
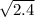
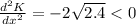
Substitute x=
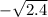
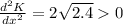
Hence, the kinetic energy is maximum at x=
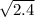
Again by work energy theorem , the maximum kinetic energy of the block between x=0 and x=2.0 m is given by
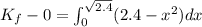
![k_f=[2.4x-(x^3)/(3)]^(√(2.4))_(0)](https://img.qammunity.org/2020/formulas/physics/college/d4p260pd3n5xts9p52j7rvdk4qomvkc7kw.png)
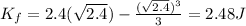
Hence, the maximum energy of the block between x=0 and x=2 m=2.48 J