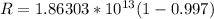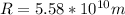Question

Suppose that a comet that was seen in 550 A.D. by Chinese astronomers was spotted again in year 1941. Assume the time between observations is the period of the comet and take its eccentricity as 0.997. What are (a) the semimajor axis of the comet's orbit and (b) its greatest distance from the Sun?

Answer 1

To solve the problem it is necessary to apply the concepts related to Kepler's third law as well as the calculation of distances in orbits with eccentricities.

Kepler's third law tells us that

`T^2 = (4\pi^2)/(GM)a^3`

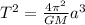
Where

T= Period

G= Gravitational constant

M = Mass of the sun

a= The semimajor axis of the comet's orbit

The period in years would be given by

`T= 1941-550\\T= 1391y((31536000s)/(1y))\\T=4.3866*10^(10)s`

PART A) Replacing the values to find a, we have

`a^3= (T^2 GM)/(4\pi^2)`

`a^3 = ((4.3866*10^(10))^2(6.67*10^(-11))(1.989*10^(30)))/(4\pi^2)`

`a^3 = 6.46632*10^(39)`

`a = 1.86303*10^(13)m`

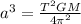
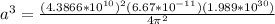
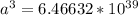
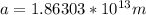
Therefore the semimajor axis is
`1.86303*10^(13)m`

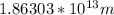
PART B) If the semi-major axis a and the eccentricity e of an orbit are known, then the periapsis and apoapsis distances can be calculated by

`R = a(1-e)`

`R = 1.86303*10^(13)(1-0.997)`

`R= 5.58*10^(10)m`