Answer:
U / K
Step-by-step explanation:
The energy stored in the capacitor is given by
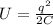
where, q be the charge and C be the capacitance of the capacitor.
If a dielctric is inserted beteen the plates of capacitor having dielctric constant K, the new capacitance is C' = KC
The charge will remain same
The new energy stored is
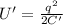
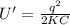
U' = U / K
So, the energy reduces by the factor of K.