Answer:
Mr. Sanchez's class sold 28 fruit pies and Mr. Kelly's class sold 32 bottles of fruit juice.
Explanation:
Let x be the number of fruit pies sold and y be the number of bottles of fruit juice sold.
Together, the classes sold 60 items, so
x + y = 60
Mr. Sanchez’s class sold fruit pies for $1.55 each, so x fruit pies cost $1.55x.
Mr. Kelly’s class sold bottles of fruit juice for $1.40 each, so y bottles of fruit juice cost $1.40y.
Together, the classes earned $88.20 for their school, so
1.55x + 1.40y = 88.20.
You get the system of two equations:
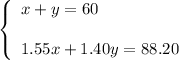
From the first equation:
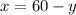
Substitute it into the second equation:
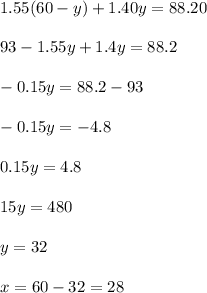
Mr. Sanchez's class sold 28 fruit pies and Mr. Kelly's class sold 32 bottles of fruit juice.