Question

A 75 kg soccer player jumps vertically upwards and heads the 0.45 kg ball as it is descending vertically with a speed of 24 m/s. If the player was moving upward with a speed of 4.0 m/s just before impact, what will be the speed of the ball immediately after the collision if the ball rebounds vertically upwards and the collision is elastic?

Answer 1

31.66 m/s

Step-by-step explanation:

mass of player, M = 75 kg

mass of ball, m = 0.45 kg

initial velocity of player, U = + 4 m/s

initial velocity of ball, u = - 24 m/s

Let the final speed of player is V and the ball is v.

use conservation of momentum

Momentum before collision = momentum after collision

75 x 4 - 0.45 x 24 = 75 x V + 0.45 x v

289.2 = 75 V + 0.45 v .... (1)

As the collision is perfectly elastic, coefficient of restitution,e = 1

So,
`e=(v_(1)-v_(2))/(u_(2)-u_(1))`

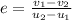
V - v = u - U

V - v = -24 - 4 = - 28

V = v - 28, put this value in equation (1), we get

289.2 = 75 (v - 28) + 045 v

289.2 = 75 v - 2100 + 0.45 v

2389.2 = 75.45 v

v = 31.66 m/s

Thus, the velocity of ball after collision is 31.66 m/.