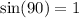Answer:
The angular momentum in this case is
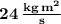
Step-by-step explanation:
The angular momentum of a point mass moving around an axis of rotation is the cross product between the distance of the object to the axis (r) of rotation and the linear momentum (p) of the particle:
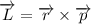 (1)
(1)
But linear momentum is defined as mv, so (1) is:
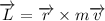 (2)
(2)
And its magnitude is:
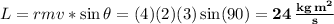 (3)
(3)
It is important to note that
 is the angle between the radius vector and the velocity vector, because the axis of rotation is perpendicular to the circle and through its center this angle is equal to 90° and
is the angle between the radius vector and the velocity vector, because the axis of rotation is perpendicular to the circle and through its center this angle is equal to 90° and