Question

the height of a triangle is 7 cm greater than the base. the area of the triangle is 147 square centimeters. find the length of the base and the height of the triangle​

Answer 1

height is 21cm and the base is 14cm

Explanation:

Take a look at the equation for the area of a triangle
`A = (bh)/(2)`

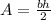
Write "height of a triangle is 7 cm greater than the base" as an equation:

h = b + 7

Substitute h and the area of the triangle, 147 into the equation for area.

`A = (bh)/(2)`

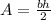
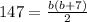`147 = (b(b+7))/(2)` distribute over brackets

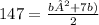`147 = (b²+7b))/(2)` get rid of fractions

`147*2 = b²+7b`

`294 = b²+7b`

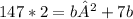
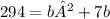
Rearrange to standard for for quadratic equations

0 = b²+7b - 294

standard form is 0 = ax² + bx + c

In this base, the x variable is replaced by "b".

Use the quadratic formula to solve for b. Substitute the other three values.

`x = \frac{-b ±\sqrt{b^(2)-4ac} }{2a}`

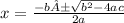
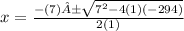`x = \frac{-(7) ±\sqrt{7^(2)-4(1)(-294)} }{2(1)}` Simplify

`x = (-7 ±√(1225) )/(2)`

`x = (-7 ±35 )/(2)`

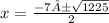
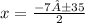
Split the equation at ±

`x = (-7 +35 )/(2)`

`x = (28)/(2)`

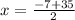
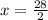
`x = 14` <=base

`x = (-7 -35 )/(2)`

`x = (-42)/(2)`

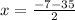
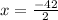
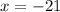`x = -21` <=We know this number is not possible, so its inadmissible.

The base is 14 cm.

Substitute base = 14 in h = b + 7

h = b + 7

h = 14 + 7

h = 21

The height is 21cm.

Therefore, the height is 21cm and the base is 14cm.