Question

A large, 68.0-kg cubical block of wood with uniform density is floating in a freshwater lake with 20.0% of its volume above the surface of the water.

You want to load bricks onto the floating block and then push it horizontally through the water to an island where you are building an outdoor grill.

a. What is the volume of the block? Express your answer with the appropriate units
b. What is the maximum mass of bricks that you can place on the block without causing
it to sink below the water surface? Express your answer with the appropriate units

Answer 1

a) V = 0.085 m^3

b) m = 17 kg

Step-by-step explanation:

1) Data given

mb = 68 kg (mass for the block)

20% of the block volume is floating

100-20= 80% of the block volume is submerged

2) Notation

mb= mass of the block

Vw= volume submerged

mw = mass water displaced

V= total volume for the block

3) Forces involved (part a)

For this case we have two forces the buoyant force (B), defined as the weight of water displaced acting upward and the weight acting downward (W)

Since we have an equilibrium system we can set the forces equal. By definition the buoyant force is given by :

B = (mass water displaced) g = (mw) g (1)

The definition of density is :

`\rho_w = (m_w)/(V_w)`

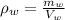
If we solve for mw we got
`m_w = \rho_w V_w` (2)

Replacing equation (2) into equation (1) we got:

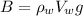`B = \rho_w V_w g` (3)

On this case Vw represent the volume of water displaced = 0.8 V

If we replace the values into equation (3) we have

0.8 ρ_w V g = mg (4)

And solving for V we have

V = (mg)/(0.8 ρ_w g )

We cancel the g in the numerator and the denominator we got

V = (m)/(0.8 ρ_w)

V = 68kg /(0.8 x 1000 kg/m^3) = 0.085 m^3

4) Forces involved (part b)

For this case we have bricks above the block, and we want the maximum mass for the bricks without causing it to sink below the water surface.

We can begin finding the weight of the water displaced when the block is just about to sink (W1)

W1 = ρ_w V g

W1 = 1000 kg/m^3 x 0.085 m^3 x 9.8 m/s^2 = 833 N

After this we can calculate the weight of water displaced before putting the bricks above (W2)

W2 = 0.8 x 833 N = 666.4 N

So the difference between W1 and W2 would represent the weight that can be added with the bricks (W3)

W3 = W1 -W2 = 833-666.4 N = 166.6 N

And finding the mass fro the definition of weight we have

m3 = (166.6 N)/(9.8 m/s^2) = 17 Kg