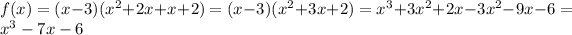Answer:
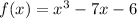
Explanation:
If x = 3 is a root of a polynomial f(x), then x - 3 is a factor of this polynomial.
If x = -2 is a zero of a polynomial function f(x), then f(-2) = 0 and x - (-2) = x + 2 is a factor of f(x).
If x = -1 is an x-intercept of the function, then y = 0 and x - (-1) = x + 1 is also a factor of the function f(x).
Therefore, the polynomial expression is
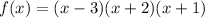
In standard form: