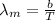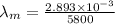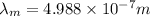Answer:
(a)
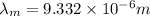
(b)
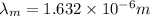
(c)
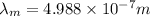
Step-by-step explanation:
According to the Wein's displacement law
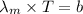
Where, T be the absolute temperature and b is the Wein's displacement constant.
b = 2.898 x 10^-3 m-K
(a) T = 37°C = 37 + 273 = 310 K
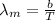
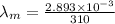
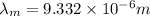
(b) T = 1500°C = 1500 + 273 = 1773 K
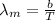
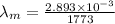
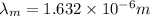
(c) T = 5800 K