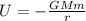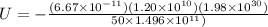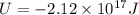Answer:
Part a)
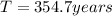
Part c)
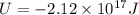
Step-by-step explanation:
Part a)
Eccentricity of ellipse is given as
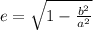
here we know that
b = 0.5 AU
a = 50 AU
so we will have
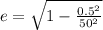
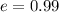
Part b)
Time period around SUN is given as
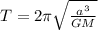
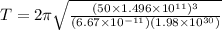
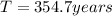
Part c)
As we know that potential energy of the system is given as