Answer:
See explanation
Explanation:
Consider triangles ADE and CBE. In these triangles,
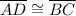 - given;
- given;
 - given;
- given;
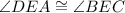 - vertical angles.
- vertical angles.
So,
 by AAS postulate. Congruent triangles have congruent corresponding parts, so
by AAS postulate. Congruent triangles have congruent corresponding parts, so
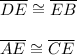
Since given
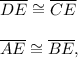
then
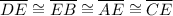
If diagonals of quadrilateral bisect each other, then this quadrilateral is a rectangle. Hence, ABCD is the rectangle.